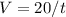Question

write a function describing the relationship of the given variables.V varies inversely with the cube of t and when t=2, V=10V=

Answer 1

To find the function of the relationship between V and t, use the following general formula, which is the formula that represents an inverse proportionality.

`xy=k`

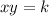
Where x and y are the variables and k is the consta t of proportionality.

In this case, the variables are V and t, it means that they will replace x and y in the formula, then, we have that:

`Vt=k`

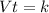
It means that the product of V and t is always the same, it is a constant named as constant of proportionality. To find k use the given values of V and t, that are 10 and 2, respectively:

`\begin{gathered} 10\cdot2=k \\ k=20 \end{gathered}`

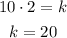
k has a value of 20, it means that the product of V and t will always be 20. It means that now, we can write an expression that relates V and t, because w know that nio matter which values have V and t, their product will always be 20, then Vt is 20:

`\begin{gathered} Vt=20 \\ V=(20)/(t) \end{gathered}`

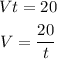
It means that the function that relates V and t is:

`V=20/t`