Question

A paper airplane is thrown off a 64-foot bridge into the water below. It’s height, in feet, is represented by f(x)= -16(x^2 - 3x - 4), where x is the number of seconds since the airplane was thrown. The height of the airplane is 0 feet when it hits the water. A. Factor the polynomial expression -16(x^2 - 3x - 4) B. Use the factorization from part A to identify the zeros of the function. C. What do the zeros mean in terms of the situation?D. Do both zeros have a real world meaning? E. How long does it take the airplane to hit the water?

Answer 1

A 64-foot bridge into the water below. It’s height, in feet, is represented by

`f(x)=-160(x^2-3x-4)`

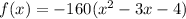
(a) The factor of the polynomials expression

`\begin{gathered} f(x)=-16(x^2-3x-4) \\ f(x)=(x^2-3x-4) \\ f(x)=(x^2+x-4x-4) \\ f(x)=(x^2+x)-(4x-4) \\ f(x)=x^{}(x+1)-4(x+1) \\ f(x)\text{ = (x+1)(x-4)} \\ \end{gathered}`

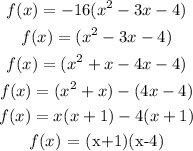
(b) Using the factorization from part A to identify the zeros of the function

`\begin{gathered} f(x)\text{ = x+1 or x-4} \\ f(x)\text{ = 0} \\ x+1\text{ = 0 or x-4 =}0 \\ x=\text{ -1 or x = 4} \end{gathered}`

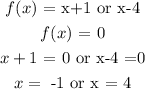
(c) Zeros of a polynomial can be defined as the points where the polynomial becomes zero as a whole. A polynomial having a value zero (0) is called zero polynomial.

Hence

`f(x)\text{ = 0}`

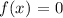
(d) Yes both zeros has a real-world meaning

(e) It took the airplane 4 seconds to hit the water since x = 4 (only positive value)