For this problem we know that the lenght of a rectangle is 7 ft less than the width who represent this equation:
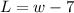
With L the lenght and w the width. We also know that the perimeter of the rectangle is given by 78 ft and we need to find the width. The perimeter is defined as:
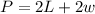
If we replace the condition of L=w-7 we got:
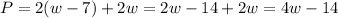
Since we know the value of the perimeter we have:
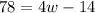
And we can solve for w and we got:

And the final answer for this case would be width =23ft