Question

try, check, and revise or write an equation to solveWhat are the two whole numbers whose product is 294 and whose quotient is 6?

Answer 1

Let the numbers are x and y

The product of the numbers = 294

So,

`x\cdot y=294\rightarrow(1)`

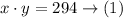
The quotient of the numbers = 6

So,

`\begin{gathered} (x)/(y)=6 \\ x=6y \end{gathered}`

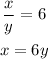
Substitute with x = 6y into the first equation:

So,

`(6y)\cdot y=294`

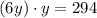
Solve for y:

`\begin{gathered} 6y^2=294 \\ y^2=(294)/(6)=49 \\ \\ y=\sqrt[]{49}=\pm7 \end{gathered}`

Now, substitute with y to find x

`\begin{gathered} y=7\rightarrow x=6y=6\cdot7=42 \\ \\ y=-7\rightarrow x=6y=6\cdot-7=-42 \end{gathered}`

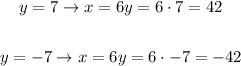
So, the answer will be:

The numbers are { 42 and 7 } or { -42, -7 }