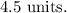Question

The question is on the picture as well as the options

Answer 1

Recall that the distance between the points after a dilation is equal to the distance before the dilation multiplied by the scale factor.

Notice that the coordinates of points P and Q are:

`P(-5,-4),\text{ Q(4,-4).}`

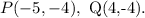
Then the original distance between the points is:

`4-(-5)=4+5=9.`

Therefore, the distance after the dilation is:

`9*(1)/(2)=4.5.`

Answer:

`4.5\text{ units.}`