ANSWER
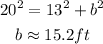
Step-by-step explanation
To find the length of the missing side, we have to apply the Pythagoras theorem:
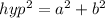
where
hyp = hypotenuse of the triangle
a and b are the length of the legs of the triangle
From the question:
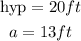
Therefore, we have that:
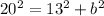
That is the equation that can be used to find the length of the missing side.
To find b, collect like terms and simplify:
![\begin{gathered} 400=169+b^2 \\ b^2=400-169 \\ b^2=231 \\ \Rightarrow b=\sqrt[]{231} \\ b\approx15.2ft \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2lpc0glkxsxwtj90wy72a3mm5q3eej0z1p.png)
That is the length of the missing side to the nearest tenth.