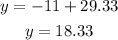Question

–2x + 2y = -22 =7x + 10y

Answer 1

The solution to the system is (29.33,18.33)So

Step by step explanation:

We have the following system of equations:

`\begin{gathered} -2x+2y=-22\text{ (1)} \\ -7x+10y=-22\text{ (2)} \end{gathered}`

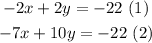
To solve the system of equations we can use the substitution method, which consists in isolate one of the variables and substitute it into the other:

`\begin{gathered} 2y=-22+2x \\ y=-11+x\text{ (1)} \end{gathered}`

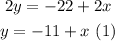
Then, we can substitute (1) into the equation (2):

`\begin{gathered} -7x+10(-11+x)=-22 \\ -7x-110+10x=-22 \\ 3x=-22+110 \\ 3x=88 \\ x=(88)/(3) \\ x=29.33 \end{gathered}`

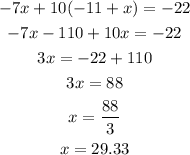
Having the x-value, we can substitute it into (1) again to get the y-value:

`\begin{gathered} y=-11+29.33 \\ y=18.33 \end{gathered}`