Given:
Dimensions are 7 ft by 5 ft by 8.5 ft
Contents weigh 0.21 pound
Contents worth $8.80 per pound
Find-: value of container contents.
Sol:
Volume is:
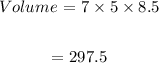
The formula of density is:
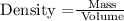
So,

Now $8.80 per pound
For 62.475 pounds the value is:
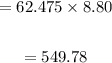
So the value of the container contents is 549.78