Since the acute angle of the given angle lies in the 3rd quadrant then
sin, cos, sec, csc will give negative values and tan and cot will give positive values
Since we have the adjacent side = -8 and the hypotenuse = 17, then
We can find cos the angle first

And sec is a reciprocal of cos (sec = 1/cos), then
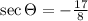
We will use the identity
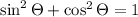
To find sin cita

Take a square root of it to find sin and take the negative value
![\begin{gathered} \sqrt[]{\sin^2\Theta}=\pm\sqrt[]{(225)/(289)} \\ \sin \Theta=-(15)/(17) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ye7n0xu2egctlau4byftlnnn8sloiog7pn.png)
As csc is the reciprocal of sin, then
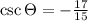
To find tan, we will use tan = sin/cos

As cot is the reciprocal of tan, then
