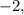![-2,\operatorname{\mid}(4)/(5)\lvert,\operatorname{\mid}\text{-1}\operatorname{\mid}\text{, }\operatorname{\mid}\text{3.5}\operatorname{\mid}\text{, }\operatorname{\mid}\text{-4.2}\operatorname{\mid}\operatorname{\lparen}\text{1st opt}\imaginaryI\text{on}\operatorname{\rparen}]()
Step-by-step explanation:
![\begin{gathered} Given: \\ |-4.2|,\text{ \mid-4/5\mid, \mid-1\mid, -2, \mid3.5\mid} \end{gathered}]()
The absolute value of a negative number gives a positive number. So we will change the negative numbers in the absolute value to positive. Afterwards, we will order the numbers
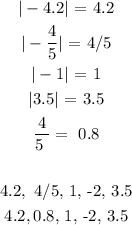
A negative number is smaller than a positve number
Ordering from lowest to highest:
-2, 0.8, 1, 3.5, 4.5
Rewriting it in the form given initially: