In order to calculate how many times one earthquake is more intense than the other, first let's calculate the intensity of each one.
To do so, let's use the definition of logarithm:
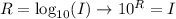
So we have:
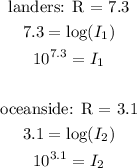
Now, to calculate the division of intensities, we can use the property below:
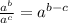
So we have:
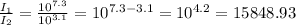
Therefore the intensity of the first earthquake was 15848.93 times higher than the intensity of the second earthquake.