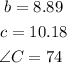 Step-by-step explanation
Step-by-step explanationthe law of sines states that
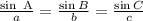
hence
Step 1
a)let
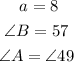
b) replace to find B
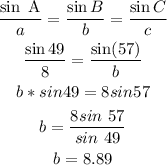
c) we can find the angle C usign the fact that the sum of the internal angles in a triangle equals 180,so
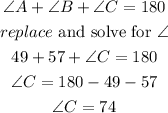
c) finally, side c
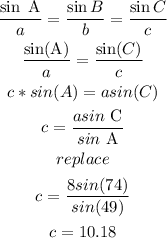
so, the answer is ( one triangle)
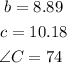
I hope this helps you