Question

Hello, how do you find the area of the indicated region between y= x^2 and y= -1 for x in [ -1, 1]

Answer 1

8/3

1) Let's calculate this area by using Integration. We have two functions:

`f(x)=x^2,g(x)=-1`

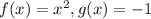
2) So let's plot them to better visualize it:

Note that we have to find the area between two curves, considering from x=-1 to x=1, so let's integrate, considering f(x) > g(x):

`\begin{gathered} A=\int ^1_(-1)(f(x)-g(x))dx \\ A=\int ^1_(-1)(f(x)-g(x))dx \\ A=\int ^1_(-1)x^2+1dx \\ A=\int ^1_(-1)x^2dx+\int ^1_(-1)1dx \\ A=(2)/(3)+2=(8)/(3) \end{gathered}`

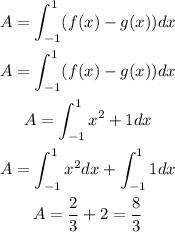
3) Hence, the area between those curves is 8/3