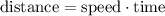
Let x be the time it takes him to get to the comic book store
Ley y be the time it takes him to return home
The distance is the sa from home to comic book store and from comic book store to home:
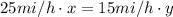
The entire travel time was 4 hours:
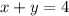
Uset he next system of equations:
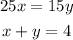
1. Solve y in the first equation:
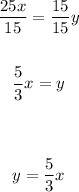
2. Use the value of y you get in step 1 in the second equation.
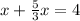
3. Solve x:
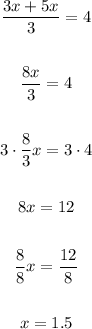
Then, the time it takes him to get to the comic book store is 1.5 hours