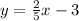when 2 lines are perpendicular the slopes are inverted and have a different sign
for example if a slope is 2, the slope of perpendicular line is -1/2
take two poins of m line (-2,2) and (0,-3)
the slope of the m line is
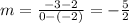
so, the slope of the perpendicular line is

now, the geberal form of the line is

where m is the slope and b the y-intercept
we replace the slope= 1/5 and repace the point (10,1) to find b
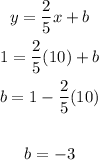
so the equation of the perpendicular line is