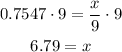To find the legs of a right triangle, you can use the following relations:
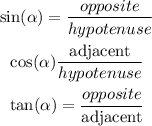
In this question, the hypotenuse and a angle of 41° is given.
You need to find x, that is, the adjacent side to 41°.
So, let's use an equation that uses information of the adjacent side and hypotenuse. This equation is:
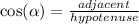
Knowing that:
α = 41°
hypotenuse = 9
Then,

Now, solve the equation.
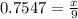
Multiplying both sides by 9: