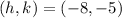Question

Determine whether the quadratic function shown below has a minimum or maximum, then determine the minimum or maximum value of the function. f(x) = (x + 8)² - 5

Answer 1

we are given the following function:

`f\mleft(x\mright)=(x+8)^(2)-5​`

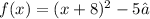
This is a function of the form:

`f(x)=a(x-h)+k`

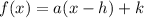
Where the point (h, k) is the vertex of the parabola that represents the graph of the function. Since the point "a" in the function is:

`a=1>0`

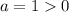
This means that the vertex is a minimum and that minimum is located at the point:

`(h,k)=(-8,-5)`