Question

An astronaut is doing a spacewalk on a long tether at 0.05 km away from an orbitingsatellite. His spacesuit includes a very sensitive gravitometer, which indicates thegravitational force acting on the astronaut and his spacesuit from the satellite is 3.34E-8 N. If the mass of the astronaut and his suit is 250 kg, what is the mass of thesatellite if G = 6.67 E-11 N'm²/kg²?5,000kg4,000kg7,000kg6,000kg

Answer 1

Answer: 5000kg

Explanation: Hope this was helpful

Answer 2

1st option: 5,000kg

Explanation:

Given:

Distance (d) = 0.05 km = 50 m

Force (F) = 3.34x10^-8

Mass of the astronaut (Ma) = 250 kg

G = 6.67 x10^-11 N'm²/kg²

We can calculate the mass of the satellite (Ms) using the following formula:

`F=(G\cdot M_a\cdot M_s)/(d^2)`

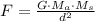
We substitute each value and solve for the mass of the satellite, just like this:

`\begin{gathered} 3.34\cdot10^(-8)=(6.67\cdot10^(-11)\cdot250\cdot M_s)/(50^2) \\ M_s=(3.34\cdot10^(-8)\cdot50^2)/(6.67\cdot10^(-11)\cdot250) \\ M_s=5007.5\cong5000kg \end{gathered}`

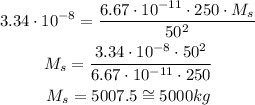
The mass of the satellite is equal to 5000 kilograms