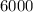Question

Find the coefficient of the x^2 term in the expansion of (5x-2)^6 //answer choices: 84, 240, 2625, and 26250

Answer 1

We are given the expression below to expand:

`(5x-2)^6`

To find the coefficient of the expansion we will need to use the formula below. The formula below indicates the binomial expansion formula

`\sum ^n_(k\mathop=0)C^n_ka^kb^(n-k)`

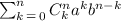
This will enable us to find the particular term we want, then we can pick out the coefficient of the term.

The parameters are as follows

n=6,k=0,1,2,3,4,5,6, a=5x i.e the first term and b =-2 i.e the second term

We will then apply parameters to the formula above.

`^6C_0(5x)^6(-2)^0+^6C_1(5x)^5(-2)^1+^6C_2(5x)^4(-2)^2+^6C_3(5x)^3(-2)^3+^6C_4(5x)^2(-2)^4+^6C_5(5x)^1(-2)^5_{_{}}+^6C_6(5x)^0(-2)^6`

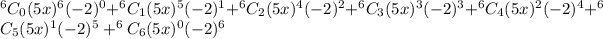
The expression above gives the interpretation of the binomial formula when the parameters are inserted.

Since we are looking for the coefficient of the x^2 we narrow it down to the term below, gotten from the expression above

`^6C_4(5x)^2(-2)^4`

We then simplify the above to get the required answer

`\begin{gathered} ^6C_4(5x)^2(-2)^4 \\ =(6!)/((6-4)!4!)*25x^2*16 \\ =(6!)/(2!4!)*400x^2 \\ =(6*5*4!)/(2*1*4!)*400x^2 \\ =3*5*400x^2 \\ =6000x^2 \end{gathered}`

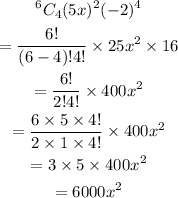
Therefore, the coefficient of the x^2 term is

`6000`