Question

Simplify the following expression. Express your answer as a single radical.

Answer 1

We can rewrite radicals as fractional exponents, like the following example

`\sqrt[y]{x}=x^{(1)/(y)}`

Using this rule in our problem, we can rewrite our expression as

`\sqrt[4]{5}\sqrt[16]{5}=5^{(1)/(4)}\cdot5^{(1)/(16)}`

When we have a product of two exponentials with the same basis, we just add the exponents.

`a^b\cdot a^c=a^(b+c)`

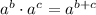
Using this property in our problem, we have

`5^{(1)/(4)}\cdot5^{(1)/(16)}=5^{(1)/(4)+(1)/(16)}=5^{(4)/(16)+(1)/(16)}=5^{(5)/(16)}=\sqrt[16]{5^5}=\sqrt[16]{3125}`

And this is our result.

`\sqrt[4]{5}\sqrt[16]{5}=\sqrt[16]{3125}`