Question

Find the area and arc length of a sector with central angle 140.

Answer 1

a Remember that

The area of complete circle is equal to

`A=\pi\cdot r^2`

The area of a complete circle subtends a central angle of 360 degrees

so

Applying proportion

Find out the area of the sector with a central angle of 240 degrees

`(\pi\cdot r^2)/(360)=(x)/(240)`

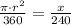
Solve for x

`x=(240\cdot\pi\cdot r^2)/(360)`

Simplify

`x=(2\cdot\pi\cdot r^2)/(3)`

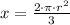
that is the area of the sector with a central angle of 240 degrees

Part b

The circumference of the complete circle is equal to

`C=2\pi r`

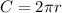
the arc length of the complete circle subtends a central angle of 360 degrees

so

Applying proportion

Find out the arc length by a central angle of 240 degrees

`(2\pi r)/(360)=(x)/(240)`

solve for x

`x=(4\pi r)/(3)`

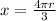
that is the arc length for a central angle of 240 degrees