The Solution:
Given that a layer of a crushed rock must be spread over a circular area of 20 feet in diameter, means that the radius of the circular area is 20 divided by 2, which gives 10 feet as radius.

We are required to find the height of a layer that gives 150 cubic feet of the rock.
This means that the layer of the rock must be cylindrical. So, by formula, the volume of a cylindrical figure is given below:

In this case,
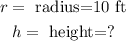
Substituting in the formula above, we get
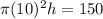
Simplifying to get the value of h, we have
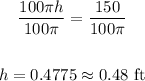
Therefore, the correct answer is 0.