Considering that the points A, B, C, and D are on the same line.
We know that C is the midpoint between A and B.
And B is between A and D.
First, let's sketch the points to visualize their positions:
The total length of the line AD is 15 units. Point B divides this line into two segments, AB and BD, so that:

From this expression, you can calculate the measure of line segment AB:
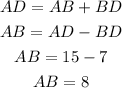
Next, if point C is the midpoint of AB, it means that it separates this segment into two equal segments AC and CB. We can calculate the length of these segments by dividing AB by 2:
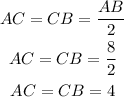
Now, what is left is to determine the length of the segment CD
Line segment CD is formed by the segments CB and BD, so that:

Line segment CD has a length of 11 units.