y=4x-28
Explanationwhen two lines are perpendicular the product o their slopes equals, -1
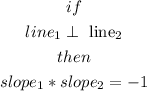
so
Step 1
find the slope of the line AC
a)the function of the line DB is given in the form
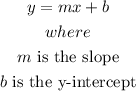
so
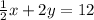
b)isolate y to get the slope-intercept form, and check the m value
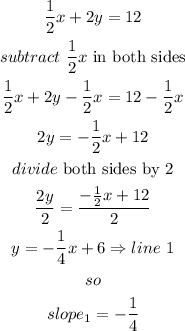
c) now, as the lines AC and DB are perpendicular replace to find slope 2
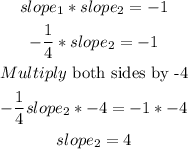
therefore
the slope of the line AC is 4
Step 2
now, we can use the slope-point formula to find the equaiton of the line,it says
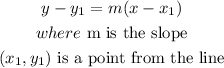
so
a)let

b) finally, replace and solve for y
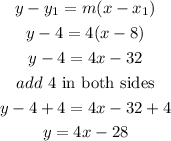
so, the equation of the line AC ia
y=4x-28
I hope this helps you