Question

Can you please help me list all limits/and check to see if my graph is missing anything

Answer 1

`y=(2x^2-5x+2)/(x^2-4)`

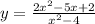
Limits:

To + infinite and - infinite limit you can evaluate the limit as follow: As you can see the limit is is the horizontal asymptote.

`\begin{gathered} \lim _(x\to\pm\infty)((2x^2-5x+2)/(x^2-4)) \\ \\ \text{Transform the equation by factoring x}^2\text{ in numerator and denominator:} \\ \lim _(x\to\pm\infty)((x^2(2-(5)/(x)+(2)/(x^2)))/(x^2(1-(4)/(x^2)))) \\ \\ \lim _(x\to\pm\infty)((2-(5)/(x)+(2)/(x^2))/(1-(4)/(x^2))) \\ \\ \text{Evaluate the limit knowinf that:} \\ \lim _(n\to\pm\infty)((1)/(n^p))=0 \\ \\ \\ \lim _(x\to\pm\infty)((2-(5)/(x)+(2)/(x^2))/(1-(4)/(x^2)))=(2-0+0)/(1-0)=(2)/(1)=2 \end{gathered}`
`\begin{gathered} \lim _(x\to-2^+)((2x^2-5x+2)/(x^2-4))=-\infty \\ \\ \lim _(x\to-2^-)((2x^2-5x+2)/(x^2-4))=+\infty \\ \\ \end{gathered}`

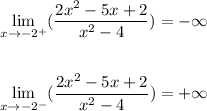
For the limits above you use the vertical asymptote (x=-2), the function tends to -infinite to the right of the asymptote and tends to + infinite to the left of the symptote

Graph: Function in red

Vertical asymptote in blue

Horizontal asymptote in green

x- Intercept (0.5,0)

y-intercept (0,0.5)