Given:
The exponential model is,
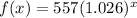
The function f(x) denotes the population of a country in millions x years after 1968.
a) Put x = 0,
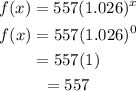
Answer: Country's population in 1968 was 557 million
b) In the year 1995 the country's population will be,
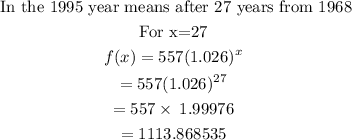
Answer: In the year 1995 the population is 1113.868535 million.