Question

a) your one friend and their bumper boat (m = 210 kg) are traveling to the left at 3.5 m/s and your other friend and their bumper boat (m = 221 kg) are traveling in the opposite direction at 1.8 m/s. The two boats then collide in a perfectly elastic one-dimensional collision. How fast is your first friend and their boat moving after the collision?

Answer 1

Given:

The mass of your first friend's bumper boat is

`m_(1i)=\text{ 210 kg}`

The speed of your first friend's boat before collision towards the left is

`v_(1i)=3.5\text{ m/s}`

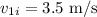
The mass of your second friend's bumper boat is

`m_(2i)=221\text{ kg}`

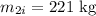
The speed of your second friend's boat before collision towards the right is

`v_(2i)=\text{ 1.8 m/s}`

The boats collided perfectly elastic.

Required:

(a) Speed of first friend's boat

Step-by-step explanation:

According to the conservation of momentum,

`\begin{gathered} m_1v_(1i)-m_2v_(2i)=m_1v_(1f)+m_2v_(2f) \\ v_(2f)=(m_1v_(1i)-m_2v_(2i)-m_1v_(1f))/(m_2) \\ =(337.2-210v_(1f))/(221) \end{gathered}`

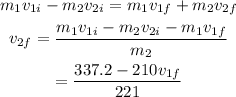
As the collision is perfectly elastic, the kinetic energy will also be conserved

`\begin{gathered} (1)/(2)m_1(v_(1i))^2+(1)/(2)m_2(v_(2i))^2=(1)/(2)m_1(v_(1f))^2+(1)/(2)m_2(v_(2f))^2 \\ m_1(v_(1\imaginaryI))^2+m_2(v_(2\imaginaryI))^2=m_1(v_(1f))^2+m_2(v_(2f))^2 \end{gathered}`

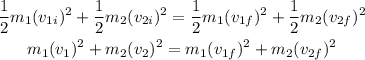
On substituting the values, the speed of the first friend's boat will be

`\begin{gathered} 210*(3.5)^2+221*(1.8)^2=210(v_(1f))^2+221*((337.2-210v_(1f))^2)/((221)^2) \\ 3288.54=210(v_(1f))^2+514.5+199.5(v_(1f))^2-640.83v_(1f) \\ 409.5(v_(1f))^2-640.83v_(1f)-2774.04=0 \\ v_(1f)=\text{ -1.94 m/s} \end{gathered}`

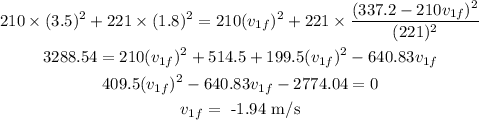
Final Answer: The speed of the first friend boat is -1.94 m/s after the collision.