Question

Ben deposited $10,000 intoeach of two savings accounts.Account 1 - 4% Compounded AnnuallyAccount 2 - 3% Compounded AnnuallyBen does not make any more depositsor withdrawals. How much more money.will be in account 1 than account 2 atthe end of 3 years?

Answer 1

The amount A earned at the end of a given period t for an interest compounded annually is expressed as

`\begin{gathered} A\text{ = P(}1+(r)/(n))^(nt) \\ \text{where} \\ A=\text{Amount} \\ P\text{ = principal (amount deposited)} \\ r=interest\text{ } \\ n\text{ = }number\text{ of times interest applied per time period} \\ t\text{ = period elapsed} \end{gathered}`

Account 1:

Amount deposited = 10000. thus, P = 10000

r = 4% = 0.04

Since the interest is compounded annually, n= 1

t = 3.

Thus, the amount in account 1 after 3 years is evaluated as

`\begin{gathered} A\text{ = P(}1+(r)/(n))^(nt) \\ A\text{ = 10000(1+}(0.04)/(1))^((1*3)) \\ =10000(1+0.04)^3\text{ } \\ =10000(1.04)^3 \\ \Rightarrow A\text{ = }11248.64 \end{gathered}`

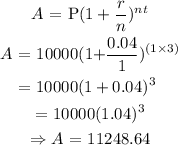
The amount earned at the end of 3 years in account 1 is $ 11248.64

Account 2:

P =10000

r = 3% = 0.03

n =1

t = 3

Thus, the amount in account 2 after 3 years is evaluated as

`\begin{gathered} A\text{ = P(}1+(r)/(n))^(nt) \\ =10000(1+(0.03)/(1))^((1*3)) \\ =10000(1+0.03)^3 \\ =10000(1.03)^3 \\ \Rightarrow A=10927.27 \end{gathered}`

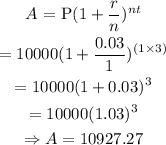
The amount earned at the end of 3 years in account 2 is $ 10927.27

How much more will be in account 1 than account 2:

`\begin{gathered} Amount\text{ earned in account 1 - amount earned in account 2} \\ $11248.64$\text{ - }$10927.27$ \\ =\text{ 321.3}7 \\ \end{gathered}`

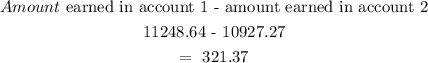
Hence, there will be $ 321.37 in account 1 than account 2.