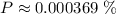You know that the number of playing cards in the deck is 52.
Then, since you need to determine the probability of being dealt 4 Aces of cards without replacement, you need to set up the following:
- The probability to get the first Ace:
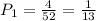
- You have 51 playing cards left. Then, the probability to get a second Ace is:
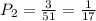
- Now you have 50 playing cards left. Then, the probability to get a third Ace is:
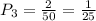
- The probability to get a fourth Ace is:

Therefore, the probability of being dealt 4 Aces of cards can be found by solving this Multiplication:
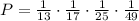
Hence, you get:
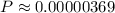
In percent form:
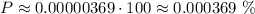
Hence, the answer is: