Question

Freida has money to invest in one of two accounts.Account 1 requires an investment of $4,600 that earns 2% interest compounded monthly for 4 years.Account 2 requires an investment of $3,000 that earns 4% interest compounded quarterly for 4 years.Freida's goal is to earn the greatest amount of profit possible.Which investment is better for Freida, and why?Select the answer that is completely correct.Account 1 is better because the final value is $1,465.05 more than the final value of Account 2 after 4 years.Either account is good because Account 1 requires more money, but the interest rate for Account 2 is higher.Account 2 is better because it earns $134.95 more in interest than Account 1 after 4 years.Account 1 is better because its ROI is 8.9% more than the ROI of Account 2 after 4 years.

Answer 1

Given:

Account 1 :

Principal amount = $ 4600

Interest = 2%

time = 4 years compounded monthly.

The future value is,

`\begin{gathered} A_1=P(1+(r)/(n))^(nt) \\ A_1=4600(1+(2)/(100*12))^(12*4) \\ A_1=4600(1+0.001666667)^(48) \\ A_1=4982.79 \end{gathered}`

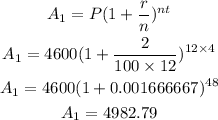
Account 2:

Principal amount = $ 3000

Interest = 4%

time = 4 years compounded quarterly.

The future value is,

`\begin{gathered} A_2=P(1+(r)/(n))^(nt) \\ A_2=3000(1+(4)/(100*4))^(4*4) \\ A_2=3000(1+0.01)^(16) \\ A_2=3517.74 \end{gathered}`

The difference between the future values of both accounts is,

`A_1-A_2=4982.79-3517.74=1465.05`

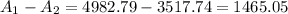
Answer: Account 1 is better because the final value is $1465.05 more than the final value of Account 2 after four years.