The Solution.
Let the number of adults that attended the show be x ;
and the number of students that attended the show be y.
Representing the problem in equations, we get
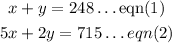
Solving the pair of equations simultaneously by elimination method:
To eliminate the terms in x, we multiply through eqn(1) by 5 to get,
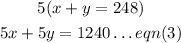
Subtracting eqn(2) from eqn(3), we get
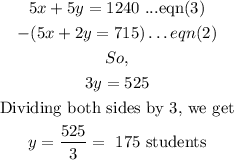
Thus, the number of students that attended the talent show is 175.