Given:
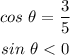
We will find the following:
A) the quadrant of the angle.
the cosine of the angle is positive in two quadrants the first and the fourth
In the first quadrant, the sine is (+v)
while in the fourth quadrant the sine is (-v)
So, for the given angle, the angle lying in Q4
B) other five trig function values.
The hypotenuse = h = 5
the adjacent = x = 3
The opposite = y = ±√(5^2 - 3^2)= ±√16 = -4
Choose the (-ve) value because the angle lying in Q4
So, the trig functions will be as follows:
