ANSWER:
$814.49
Explanation:
Given:
Principal (P) = $3000
Rate (r) = 1.5%
Tim (t) = 4
For continuously compounded formula is the following:

This means after 4 years Trafton has $3185.51 in his savings account, what he needs to get up to $4000 is calculated by the following subtraction:
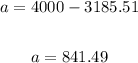
This means that he needs an additional $814.49 to buy the car.