Question

Can someone help me with this question? I’m not sure how to do it

Answer 1

`\begin{gathered} \text{Sum}=(8)/(5x) \\ \text{Domain}=(-\infty,0)\cup(0,\infty) \end{gathered}`

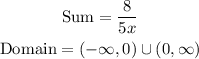
Step-by-step explanation

Given the sum of fraction;

`(1)/(x)+(3)/(5x)`

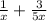
To get the domain of the function, we need to get all the input variable "x" for which the expression exists.

The function will exist when x ≠ 0 i.e. x < 0 and x > 0

The domain of the expression in interval notation is

`D=(-\infty,0)\cup(0,\infty)`

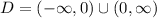
Solve the given expression

`\begin{gathered} =(1)/(x)+(3)/(5x) \\ =(5+3)/(5x) \\ =(8)/(5x) \end{gathered}`

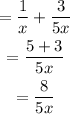
Hence the sum of the indicated operation is 8/5x