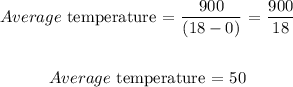Question

during a certain 18 hour period the temperature at time t (measured an hours from the start of the period) was T(t)=50+6t-1/2t^2 degrees. what was the average temperature during that period? (simplify)

Answer 1

Answer:
`Average\text{ temperature during that period = 50\degree}`

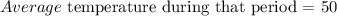
Step-by-step explanation:
`\begin{gathered} T(t)\text{ = 50 + 6t - }(1)/(2)t^2 \\ duration\text{ = 18 hr period} \end{gathered}`

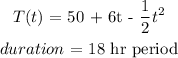
To find the average temperature, we will integrate the temperature function over the interval 18 hour period (that is from 0 to 18)

`\begin{gathered} Average\text{ value = }\int_0^(18)(50\text{ + 6t - }(1)/(2)t^2)dt \\ =\int_0^(18)50\text{ dt+ 6tdt - }(1)/(2)t^2dt \\ =[50t\text{ + }(6t^2)/(2)\text{- }(1)/(2)(t^3)/(3)]\text{ interval 0 to 18} \\ =[50t\text{ + 3t}^2\text{ - }(t^3)/(6)]\text{ interval 0 to 18} \end{gathered}`
`\begin{gathered} substitute\text{ the intervals:} \\ =\text{ \lbrack50\lparen18\rparen+ 3\lparen18\rparen}^2\text{ - \lparen}(18^3)/(6))]\text{ - \lbrack50\lparen0\rparen+ 3\lparen0\rparen}^2\text{ - \lparen}(0^3)/(6))]\text{ } \\ =\text{ 900 + 972 - 972 - 0} \\ Average\text{ value }=\text{ 900} \end{gathered}`

The average temperature will be the average value gotten above divided by the time period

`\begin{gathered} Average\text{ temperature = }(900)/((18-0))\text{ = }(900)/(18) \\ \\ Average\text{ temperature = 50\degree} \end{gathered}`