Question

According to a report from a particular university, 11 3% of female undergraduates take on debt. Find the probability that exactly 4 female undergraduates have taken on debt if 50female undergraduates were selected at randomWhat probability should be found?1 - P(4 female undergraduates take on debt)P(1 female undergraduate takes on debt)1.P4 female undergraduates take on debt)P(4 temale undergraduates take on debt)The probability that exactly 4 temale undergraduates take on debt is(Type an integer or decimal rounded to three decimal places as needed)Help Me Solve ThisView an ExampleGet More HelpClear A

Answer 1

From the given, let n = 50, x = 4, p = 0.113, and q = 1-0.113 = 0.887.

Since we need to find the probability that exactly 4 of the respondents are on debt, we need to look for P(4). Thus, we need to look for P(4 female undergraduates take on debt).

To obtain this, substitute the given values into the binomial probability formula.

`P(x)=_nC_xp^xq^(n-x)`

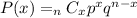
Thus, we have the following.

`\begin{gathered} \\ P(4)=_(50)C_4(0.113)^4(0.887)^(50-4) \end{gathered}`

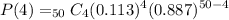
Simplify the combination and the exponenial expressions.

`\begin{gathered} P(4)=(230300)(0.113)^4(0.887)^(50-4) \\ =(230300)(0.113)^4(0.887)^(46) \\ \approx(230300)(0.000163047361)(0.004022411635) \end{gathered}`

Simplify the expression. Multiply.

`\begin{gathered} P(4)\approx0.1510407815 \\ \approx0.151 \end{gathered}`

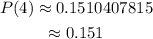
Therefore, the probability that exactly 4 female undergradraduates take on debt is about 0.151.