Question

Susan has $2.40 in nickels, dimes and quarters. She has two more dimes than nickels and four morequarters than nickels. How many types of each coindoes Susan have?

Answer 1

To solve this problem, we have to use the equivalence of each type in dollars.

Taking x, y and z as the number of nickels, dimes and quarters, we have that:

`0.05x+0.1y+0.25z=2.40`

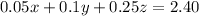
0.05 is the equivalence of one nickel in dollars, same for 0.1 and 0.25 with dimes and quarters respectively.

Now, we know that she has 2 more dimes than nickels:

`y=x+2`

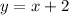
And 4 more quarters than nickels:

`z=x+4`

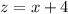
We can use the expression for y and z in terms of x in the first equation to find the value of x (number of nickels):

`\begin{gathered} 0.05x+0.1(x+2)+0.25(x+4)=2.40 \\ 0.05x+0.1x+0.2+0.25x+1=2.40 \\ 0.4x+1.2=2.40 \\ 0.4x=2.40-1.20 \\ 0.4x=1.20 \\ x=(1.20)/(0.4) \\ x=3 \end{gathered}`

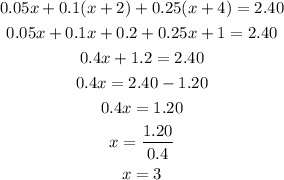
Once we have found x, we can use it to find y and z using the equations we stated:

`\begin{gathered} y=x+2 \\ y=3+2 \\ y=5 \\ z=x+4 \\ z=3+4 \\ z=7 \end{gathered}`

It means that Susan has 3 nickels, 5 dimes and 7 quarters.