Question

Can you help me out with a question

Answer 1

First, we find the area of the square knowing that its side length is 22 feet.

`A_{\text{square}}=(22ft)^2=484ft^2`

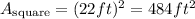
The area of an equilateral triangle is

`A_{\text{equilateral}}=\frac{\sqrt[]{3}}{4}a^2`

Where a = 22 ft.

`A_{\text{equilateral}}=\frac{\sqrt[]{3}}{4}\cdot(22ft)^2=\frac{484\sqrt[]{3}}{4}ft^2=121\sqrt[]{3}ft^2`

Then, we find the area of the right triangle

`A_{\text{right}}=(bh)/(2)=(16ft\cdot22ft)/(2)=176ft^2`

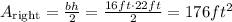
At last, we add all three areas

`A=484ft^2+121\sqrt[]{3}ft^2+176ft^2\approx869.6ft^2`

Hence, the area of the composite figure is 869.6 square feet.