Given that they performed 14 manicures and 1 pedicure, bringing in a total of $206 in receipts. and they have administered 31 manicures and 1 pedicure, with receipts totalling $427. The salon charges for a manicure and for a pedicure can be derived below.
Explanation
Let the charges for a manicure and for a pedicure be x and y respectively
Therefore, the system of equations can be derived as;

In augumented matrix form, this can be expressed as;

Here we perform the row operation:
R1→ R1 - R2
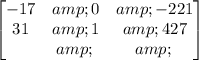
R1→ 1/-17.R1
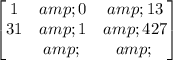
R2→ R2 - 31R1
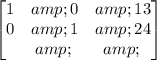
Thus the last column represents the values of the variables and we have x = 13, and y = 24
Answer: Therefore, the salon charges 13 dollars for a manicure and 24 dollars for a pedicure