Question

X²+2x-24=f(x)what is the solution

Answer 1

We are given the following quadratic equation

`f(x)=x^2+2x-24`

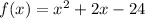
We can solve this equation by factoring or by using the quadratic formula.

Let us solve the equation by factoring.

We need two numbers such that their product is -24 and their sum is 2

a×b = -24

a + b = 2

How about 6 and -4?

a×b = 6×-4 = -24

a + b = 6 - 4 = 2

Now break the middle term (2x) as (6x - 4x)

`\begin{gathered} x^2+2x-24 \\ (x^2+6x)-(4x-24) \end{gathered}`

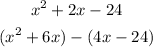
Take x common from the first pair and -4 from the second pair

`\begin{gathered} (x^2+6x)-(4x-24) \\ x(x+6)-4(x+6) \\ (x+6)(x-4) \end{gathered}`

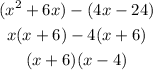
So, the solution is

`\begin{gathered} x+6=0\: \: and\: \: x-4=0 \\ x=-6\: \: and\: \: x=4 \end{gathered}`

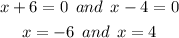
Therefore, the solution of the given quadratic equation is

`(-6,4)`