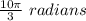Question

Answer the following. (a) Find an angle between 0° and 360° that is coterminal with - 58°. 16л (b) Find an angle between 0 and 2π that is coterminal with 16pie/3 Give exact values for your answers.

Answer 1

(a) Given that the angle must be coterminal with this other angle:

`-58\text{\degree}`

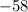
By definition, Coterminal Angles have the same initial side and they also have the same terminal side.

In this case, knowing that the angle must be between these angles:

`0\text{\degree and }360\text{\degree}`

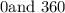
You can find it by adding 360 degrees to the given angle:

`-58\text{\degree}+360\text{\degree}=302\text{\degree}`

(b) Given the angle:

`(16\pi)/(3)`

You know that the coterminal angle must be between:

`0\text{ and }2\pi`

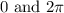
Therefore, you can find it as follows:

`(16\pi)/(3)-2\pi=(16\pi-(3)(2\pi))/(3)=(10\pi)/(3)`

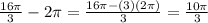
Hence, the answers are:

(a)

`302\text{\degree}`

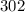
(b)

`(10\pi)/(3)\text{ }radians`