Question

How do I sketch the graph for y= -1/2x + 3 ?

Answer 1

The Slope-Intercept form of the Equation of the line is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

For the equation:

`y=-(1)/(2)x+3`

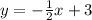
You can identify that the y-intercept is:

`b=3`

Since the line cuts the y-axis when "x" is zero, you have this point:

`(0,3)`

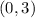
Since the line cuts the x-axis when "y" is zero, you can substitute this value into the equation and solve for "x":

`\begin{gathered} 0=-(1)/(2)x+3 \\ -3=-(1)/(2)x \\ (-3)(-2)=x \\ x=6 \end{gathered}`

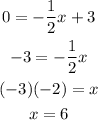
Now you have this point:

`(6,0)`

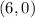
Plot both points on the Coordinate plane and graph the line. See the picture attached: