ANSWER
y = -1.2x - 2
Step-by-step explanation
We want to find the equation of the line that passes through points (-5, 4) and (5, -8).
To do this, we use the formula:
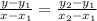
From the question:
x1 = -5
y1 = 4
x2 = 5
y2 = -8
Therefore:
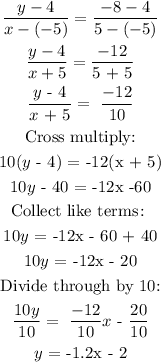
That is the equation of the line that passes through those points.