Question

The height of a javelin after it has left the hand of the thrower can be modeled by the function ℎ = −3(4t+ 2)(t− 4), where ℎ is the height of the javelin and t is the time in seconds. Determine how many seconds the javelin is in the air for. Use any strategy of your choice.

Answer 1

The height of the javelin is modeled by the function:

`h(t)=-3(4t+2)(t-4)`

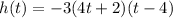
This function is a quadratic function, where t (time in seconds) represents the variable on the x-axis, and h (height) represents the variable on the y-axis.

The javelin remains a determined time t on the air and when it reaches the ground, the height is equal to zero. This point represents the right x-intercept (or root) of the quadratic function.

To determine the roots of the quadratic function, first, you have to write it in standard form. To do so you have to distribute the multiplication on the parentheses terms, that is, multiply each term of the first parentheses by each term on the second parentheses:

`\begin{gathered} h(t)=-3(4t+2)(t-4) \\ h(t)=-3(4t\cdot t+4t\cdot(-4)+2\cdot t+2\cdot(-4)) \\ h(t)=-3(4t^2-16t+2t-8) \\ h(t)=-3(4t^2-14t-8) \end{gathered}`

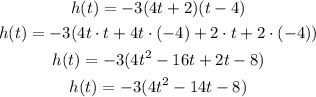
Next, multiply each term inside the parentheses by -3:

`\begin{gathered} h(t)=-3(4t^2-14t-8) \\ h(t)=-3\cdot4t^2-14t\cdot(-3)-8\cdot(-3) \\ h(t)=-12t^2+42t+24 \end{gathered}`

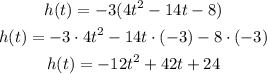
Once you have written the quadratic function on the standard form, you have to equal the function to zero and use the quadratic formula to determine the roots of the parabola:

`-12t^2+42t+24=0`

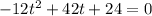
The coefficients of the quadratic function are:

a=-12

b=42

c=24

Using the quadratic formula:

`x=\frac{-b\pm\sqrt[]{(b^2)-4ac}}{2a}`

Replace the formula and solve:

`\begin{gathered} x=\frac{-42\pm\sqrt[]{42^2-4\cdot(-12)\cdot24}}{2\cdot(-12)} \\ x=\frac{-42\pm\sqrt[]{1764+1152}}{-24} \\ x=\frac{-42\pm\sqrt[]{2916}}{-24} \\ x=(-42\pm54)/(-24) \end{gathered}`

Now, let's calculate both roots:

-Addition

`\begin{gathered} x=(-42+54)/(-24) \\ x=(12)/(-24)=-(1)/(2) \end{gathered}`

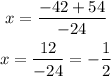
-Subtraction

`\begin{gathered} x=(-42-54)/(-24) \\ x=(-96)/(-24)=4 \end{gathered}`

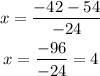
The left root of the parabola is (-1/2,0) and the right root is (4,0)

Considering that the starting point is a t=0 (when the javelin was thrown), then the time where it lands after it was thrown will be represented by the right root of the parabola (4,0).

These coordinates indicate that the javelin will reach the ground 4 seconds after being thrown, which means that it was in the air for 4 seconds.