Given:
Probability of Indiana rivers State College students plan to go on a vacation after graduation is(P) 70%=0.7.
Sample size =n=5
x= the random sample of number of students that plans to go on a vacation after graduation out of the sample of 5
The formula for binomial distribution is,
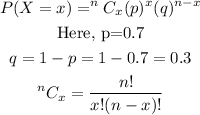
The probability that no more than 4 students out of random sample of 5 students plan to go on vaccination after graduation is given by,
![\begin{gathered} P(X\leq4)=P(X=0)+P(X=1)+P(X=2)+P(X=3)+P(X=4) \\ =^5C_0(0.7)^0(0.3)^(5-0)+^5C_1(0.7)^1(0.3)^(5-1)+^5C_2(0.7)^2(0.3)^(5-2)+^5C_3(0.7)^3(0.3)^(5-3)+^5C_4(0.7)^4(0.3)^(5-4) \\ =0.0024+0.0284+0.1323+0.3087+0.3602 \\ =0.832 \end{gathered}]()
Hence, the probability P(X≤4)=0.832.