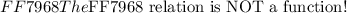Question

The domain of a relation is {-1,2,3,6}. The range of the function is {-2,-1,2,3,4}. Is it possivle for the relation to be a function?

Answer 1

We will investigate the property of a function.

A function is defined as " Each input of a function there must only be a unique output ".

On a graph this can be defined by a vertical line test. All functions must qualify the vertical line test! The test is basically scoring vertical lines on a gragh plot of a relationhsip. No vertical line must cross or meet or cut the graph at more than one point for the relationhsip to be classified as a "function".

The input values ( domain ) and output value for each are expressed below:

`\begin{gathered} \text{ }\text{\textcolor{#FF7968}{Domain : }}\left\lbrace \text{ - 1 , 2 , 3 , 6 }\right\rbrace \\ \text{\textcolor{#FF7968}{Range:}}\text{ }\left\lbrace \text{ -2 , -1 , 2 , 3 , 4 }\right\rbrace \end{gathered}`

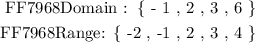
The total number of domain values are ( 4 ), where the total number of range values are ( 5 ).

The above statement implies that for any one of the domain value has two values of output value.

The above statement is a direct negation of the definition of what constitute a function f ( x ) i.e:

Therefore, the given expression is:

`\textcolor{#FF7968}{The}\text{\textcolor{#FF7968}{ relation is NOT a function!}}`