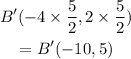Question

(1)Find the coordinates of A' given a dilation of 2A(3,-6), B(0,9), C(2,-1)(2)Find the coordinates of B' given a dilation of 1/4.A(4,-8), B(2,-4), C(0,4)(3)Find the coordinates of C' given k=3.A(3,-6), B(0,9), C(2,-1)(4)Find the coordinates of B' given k=2 1/2A(6,0), B(-4,2), C(-8,-2)

Answer 1

Part 1

Given the coordinates of ABC

A(3,-6), B(0,9), C(2,-1)

If you dilate the figure by a scale factor of 2. the coordinates of A' will be:

`\begin{gathered} A^(\prime)(3*2,-6*2) \\ =A^(\prime)(6,-12) \end{gathered}`

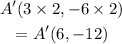
Part 2

Given the coordinates of ABC

A(4,-8), B(2,-4), C(0,4)

If you dilate the figure by a scale factor of 1/4. the coordinates of B' will be:

`\begin{gathered} B^(\prime)(2*(1)/(4),-4*(1)/(4)) \\ =B^(\prime)((1)/(2),-1) \end{gathered}`

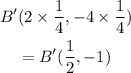
Part 3

Given the coordinates of ABC

A(3,-6), B(0,9), C(2,-1)

If you dilate the figure by a scale factor of 3. the coordinates of C' will be:

`\begin{gathered} C^(\prime)(2*3,-1*3) \\ =C^(\prime)^{}(6,-1) \end{gathered}`

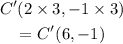
Part 4

Given the coordinates of ABC

A(6,0), B(-4,2), C(-8,-2)

If you dilate the figure by a scale factor of 2 1/2. the coordinates of B' will be:

`\begin{gathered} B^(\prime)(-4*(5)/(2),2*(5)/(2)) \\ =B^(\prime)(-10,5) \end{gathered}`