We are given angle measures in radians (represented with the pi symbol) and we need to determine in which quadrant will the terminal ray be for each angle.
Before we get started we need to know that the coordinate plane has 4 quadrants as shown in the following diagram:
Also, at 90° we have pi/2, at 180° we have pi and at 270° we have 3pi/2.
We can represent this as decimal numbers so it would be easier for us to determine where each angle is:
Step 1. Let's start with the first angle:
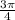
In decimal, this is equal to:
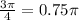
0.75 is between 0.5 and 1, thus the terminal ray of this angle will be in quadrant 1.
Step 2.
The second angle is:
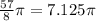
As you can see, this number is more than 2, which means that this angle will turn around the plane. We can represent it as follows:
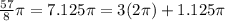
And we don't pay attention to the multiple of 2pi, but only to the second term:
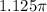
The terminal ray of this angle will be located in the third quadrant.
Step 3. We do the same as in step 2, represent the number as a decimal number, and if this number is larger than 2, we separate it as a multiple of 2pi and another term:
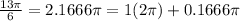
0.1666pi is between 0 and 0.5pi. The terminal ray of this angle will be in the first quadrant.
Step 4.
The next angle is:
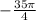
In this case, the angle is negative, so we will not be turning anti-clockwise in the coordinate plane, this time and for each negative angle, we will turn clockwise in the coordinate plain. Here we have a diagram for reference:
Again we separate the angle as a multiple of 2pi and another term:
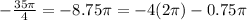
Since -0.75pi is between -0,5pi and -pi, the terminal ray of this angle is in the third quadrant.
Step 5.

represented as a decimal number:
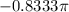
This is located in the third quadrant.
Step 6.
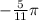
Represented as a decimal:
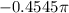
Since this number is between 0 and -0.5, the terminal ray of the angle will be located in the fourth quadrant.
Answer:
