Step 1
Write the sample space.
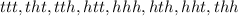
Therefore, the probability of getting 3 heads(hhh) is given as

Step 2
Find the probability of not tossing 3 heads with three fair coins is given as;
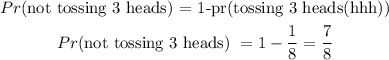
Hence, the probability of not tossing 3 heads with three fair coins = 7/8