Question

Please help me with this . Like on normal graph paper possible like the square one?

Answer 1

We are given the following function:

`f(x)=\sqrt[3]{x}`

If we want to stretch a graph vertical we must multiply the function by the factor we want to stretch it:

`g(x)=kf(x)`

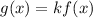
Therefore, if we want to stretch the given function by a factor of 4 we must multiply the given function by 4:

`g(x)=4\sqrt[3]{x}`

To shrink the function horizontally we must do the following change:

`g(x)=f((x)/(k))`

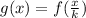
Therefore, the new function must be:

`g(x)=4\sqrt[3]{(x)/((1)/(3))}`

Simplifying we get:

`g(x)=4\sqrt[3]{3x}`

Now, we graph both functions. We get:

The blue graph represents the original function, and the green graph represent the modified function